By showing the overlap and not including any states in the overlap, it draws extra attention to the point of diagram which is that there isn’t any overlap.
A Venn diagram does not imply that the intersection of the two sets is nonempty. It is merely a visual aid to illustrate the contents of two sets, and the center part is the intersection of those sets, which can be the empty set if the sets are disjoint (as they are in this context). The use of a Venn diagram is often used to show similarities and differences between two sets, but in this case the lack of any shared elements is actually the focal point of the diagram, used to illustrate a point. Showing disjoint sets disconnected from one another doesn’t send merely as powerful of a message as showing disjoint sets in a Venn diagram, as the Venn diagram highlights the fact that they have no common elements. The reader is immediately drawn to the center of a Venn diagram when one is shown, and given that the center has no labels, it is a quick and effective way to illustrate that the sets are disjoint, especially when the reader notices how many labels exist in either set.
The essential point here is that the use of a Venn diagram does not imply shared members, it merely implies that sets are being compared.
Eh, in this instance I disagree.
By showing the overlap and not including any states in the overlap, it draws extra attention to the point of diagram which is that there isn’t any overlap.
deleted by creator
A Venn diagram does not imply that the intersection of the two sets is nonempty. It is merely a visual aid to illustrate the contents of two sets, and the center part is the intersection of those sets, which can be the empty set if the sets are disjoint (as they are in this context). The use of a Venn diagram is often used to show similarities and differences between two sets, but in this case the lack of any shared elements is actually the focal point of the diagram, used to illustrate a point. Showing disjoint sets disconnected from one another doesn’t send merely as powerful of a message as showing disjoint sets in a Venn diagram, as the Venn diagram highlights the fact that they have no common elements. The reader is immediately drawn to the center of a Venn diagram when one is shown, and given that the center has no labels, it is a quick and effective way to illustrate that the sets are disjoint, especially when the reader notices how many labels exist in either set.
The essential point here is that the use of a Venn diagram does not imply shared members, it merely implies that sets are being compared.
Literally it’s a thing: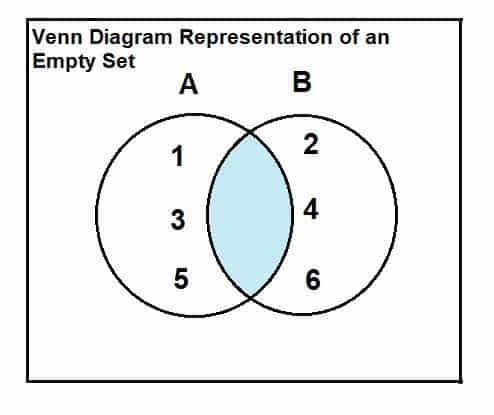
A = {1, 3, 5}
B = {2, 4, 6}
A ∩ B = ∅