19·
22 hours agoI had someone I’ve never talked to visibly confused on what pronouns to use for me. Is it literally just the longer hair???
yewler [she/her]
- 0 Posts
- 212 Comments
Joined 3 months ago
Cake day: August 23rd, 2024
You are not logged in. If you use a Fediverse account that is able to follow users, you can follow this user.
I got told one time that I’d be a cute girl if I was one and that did something to me. It’s impressive how long I was able to hold out before realizing my transness
I don’t get it
poo poo
I’m looking up at the mirror on my bedroom door and I see a girl on her bed. It’s freaking me out a bit but in a good way. This same human I’ve become so acquainted with seeing, I’m actually successfully conceptualizing her as a woman without going “ughghg but I look like a guy.” This is so bizarre, but sooooooo cool
To be fair the actual discussion did start with what was essentially a nvm lol
I can nvm lol the original nvm lol if that counts
It was something like “okay well if you ever change your mind, let me know”
My sister is great and I was immediately talking to her about gender stuff once I began seriously questioning again. I actually just got off a phone call with her right before I made that post on this com that brought me into tracha and eventually here.
Thinking about the time I texted my sister “okay but what if I was trans” one evening, and then the next morning followed it up with a good 'ol “lol nvm.”
And now here we are like a year later.
Everything I own is transitioning with me. I’ve noticed I use she/her for all of my inanimate belongings now
I really wish I lived in a world where the rizzler was on jimmy fallon. Idk why this is on the mind.
I tried looking around on YouTube for voice stuff but I wasn’t really sure what I was looking for, and I’m scared of hurting myself. I’m not really sure how to do it safely. Are there any resources you would specifically recommend?
dysphoria
I have come to realize that I am significantly more affected by dysphoria than I thought. I realized how much of a prison guyness feels like and how much I hate feeling like one. I feel like I’m always a little bit aware of what I look like and what I sound like and it makes human interaction feel so much harder.
Your area must have a much better relationship with math than mine. I and so many of my peers learned FOIL as the way you multiply binomials, with no discussion as to why. Math ed where I’m from is littered with this kind of thing. It’s incredibly frustrating.
I have never once realized I was being flirted with. Every single time I’ve become privy to that knowledge it’s been after the fact when someone else told me what was happening. I’m so goddamn oblivious.
I almost need people to stop mid flirt with a “just so you know, this is flirting.”
It’s too late. The hate train has left the station. Forgive me for doxxing myself as I send a selfie of myself on my way to fuck your shit up
As long as I get dibs I’m happy
Disclaimer: please do not misconstrue this reply as evidence that I do not hate your guts. I definitely still do
My hot take is that math class doesn’t do the one thing that justifies its place in core curriculum. We’re told that the reason we all have to take math is to strengthen our logical thinking skills so that we can apply it to life. Sort of like how you can go to the gym and lift weights, and the ability to lift them isn’t inherently useful to you, but you’re keeping yourself healthy and building muscles that you can use elsewhere in life. Everyone needs to know how to think, regardless of what you do in life, and in theory mathematics is a great “gymnasium” to practice that skill.
But is it doing that? In my experience, it doesn’t. Not even in the slightest. Being told a formula or algorithm, lectured on exactly how it works and how to use it, and then being given homework that drills your ability to apply this new concept 20 times or so does nothing for a person’s ability to think. All this requires is blind rule following with essentially no real purpose in sight. This ends up alienating many students who don’t care, have no reason to care, and have a hard time learning things they don’t care about. Math class is boring as shit, if we’re being entirely honest, but it doesn’t have to be that way.
Fundamentally, above all else, mathematics is a creative art. Painters are artists who express themselves through the medium of pigment. Musicians are artists who express themselves through the medium of rhythmic sound. Mathematicians are artists who express themselves through the medium of thought. As such, math class should function like an art class. Students should be given the reigns to be able to do their own thinking. They should be able to create their own ideas and make their own art. Genuinely fuck the quadratic formula, fuck the Pythagorean Theorem, fuck difference of squares. So few people have any reason to care about these things. Are they wonderful pieces of math that have their own wonderful nuggets worth studying? Hell yeah. But if a student has no reason to care, in my opinion they should be allowed to think about what they want to think about, to express themselves through mathematics in their own way, and in doing so, strengthen their thinking muscles the way math class should be helping them to do.
Finally getting to your actual question, the only thing I care about is if the thing the student is using is something they’ve thought about themselves (almost certainly with instructor assistance). They need to have done some of their own thinking. FOIL is just a series of letters in an order, and I don’t imagine a student is going to divine that from thin air. The box is closer to what I’d want to see, since it demonstrates actual mathematical conceptualization, but it ruins everything if the teacher just shows the box and tells the student to learn it.
One progression that a student may go though to discover this type of stuff for themselves is by thinking about multiplication. Say I want to do 6*32 in my head. That’s kind of a pain in the ass, so what can we do? Maybe with a little help (and a few drawn rectangles) they can see that it’s a lot easier to do 6*30 and add it to 6*2. That’s pretty neat. We’ve turned something I probably needed a pencil and paper or calculator for into something that’s quite easy. But there’s nothing special about this number problem is there? Thinking about this, a student may discover distributive property for themselves. In standard mathematics, we symbolize that as a(b+c) = ab + ac for all a,b,c, but the student may symbolize it another way. They may even just say it as a sentence or paragraph, and that’s okay because they have an actual concept in their mind that is tangible to them. Okay then what about (a + b)(c + d)? Well a+b is just a number, so we can use our neat little property:
(a + b)(c + d) = (a + b)c + (a + b)d = ac + bc + ab + bd
Three applications of our fancy new trick and what do we have? FOIL!
Okay but what about trinomials?
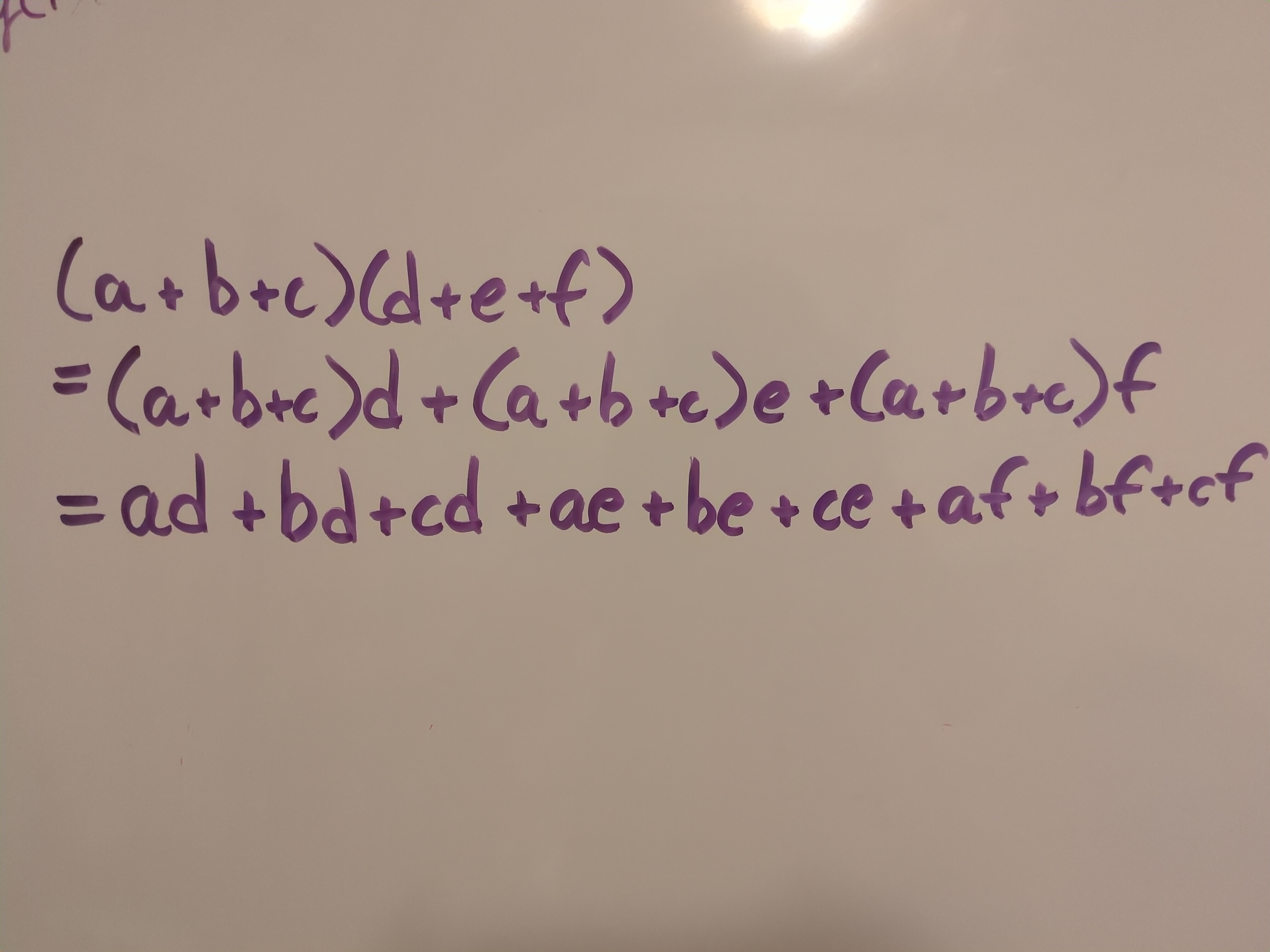
Using the fancy trick 4 times spits it right out. A student may notice they’re just multiplying everything in the first bit by everything in the second and adding everything together and can explore whether or not this works in general.
Would this style of math class slow content learning down big time? Ohhh yes, and there’s a conversation to be had about how to fit this into a world where more advanced math is useful for a lot of people, but for everyone else, there’s no reason anyone should be graduating high school with calculus under their belt. If we took our time with math ed instead of trying to over standardize an art form, we’d have better thinkers.
Math class kills the very thing it aims to build up, and I’m sick of it.
Huh. I actually feel gay. That’s a new one. It’s hard to describe since literally nothing’s changed except the word lesbian feels right now. I don’t have to be jealous of lesbians anymore!